Durbin-Watson

-

    Durbin-Watson es una estadística que se utiliza para probar la autocorrelación de los residuos en un modelo de regresión. Esta estadística se basa en la idea de que los residuos de un modelo de regresión deben ser independientes y no correlacionados.

    El valor de Durbin-Watson oscila entre 0 y 4, y cuanto más cercano esté a 2, menor será la autocorrelación. Un valor de 2 indica que no hay autocorrelación, un valor menor que 2 indica autocorrelación positiva, mientras que un valor mayor que 2 indica autocorrelación negativa.

La interpretación del valor de Durbin-Watson es la siguiente:

  • Si el valor está entre 0 y 2, hay evidencia de autocorrelación positiva en los residuos.
  • Si el valor está cerca de 2, no hay evidencia de autocorrelación.
  • Si el valor está entre 2 y 4, hay evidencia de autocorrelación negativa en los residuos.

    Es importante tener en cuenta que Durbin-Watson es una prueba de autocorrelación de primer orden, lo que significa que solo mide la correlación entre residuos adyacentes. Si hay una autocorrelación de orden superior, se necesitará una prueba diferente para detectarla.

    En resumen, Durbin-Watson es una herramienta útil para verificar la presencia de autocorrelación en los residuos de un modelo de regresión. Un valor cercano a 2 indica que los residuos son independientes y no correlacionados, lo que respalda la validez del modelo.


Ejemplo:

Supongamos que tenemos el siguiente modelo de regresión lineal simple:

y_i = β_0 + β_1 x_i + ε_i

    Donde y_i es la variable dependiente, x_i es la variable independiente, β_0 y β_1 son los parámetros desconocidos que se estiman a través del modelo y ε_i es el término de error.

    Para verificar la autocorrelación de los errores, podemos utilizar la estadística de Durbin-Watson. Supongamos que hemos obtenido los siguientes valores del modelo:

  • Valor observado de la estadística de Durbin-Watson (d): 1.76
  • Número de observaciones (n): 50

    Para probar la hipótesis nula de no autocorrelación (H0: ρ = 0) contra la alternativa de autocorrelación (H1: ρ > 0 o ρ < 0), debemos comparar el valor observado de d con los valores críticos de Durbin-Watson en una tabla o utilizando un software estadístico.

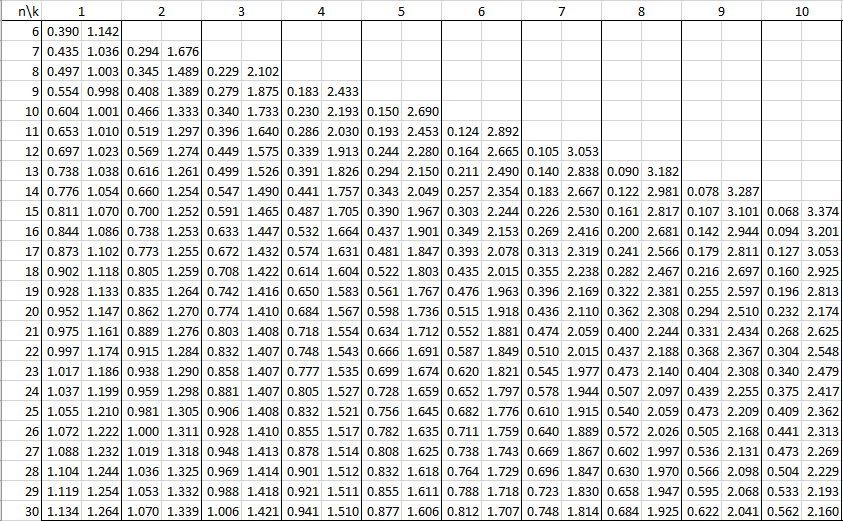
    En este ejemplo, supongamos que hemos encontrado que para un nivel de significancia del 5% y 2 grados de libertad (k = 2), los valores críticos de Durbin-Watson son d_L = 0.65 y d_U = 1.53.

    Como el valor observado de d (1.76) está por encima del valor crítico superior (d_U = 1.53), podemos rechazar la hipótesis nula y concluir que existe evidencia estadística de autocorrelación positiva en los errores del modelo. Esto indica que los errores están correlacionados entre sí y que el modelo de regresión lineal simple no es el adecuado para modelar la relación entre las variables y_i y x_i.





Comentarios

Publicar un comentario

Entradas populares de este blog

Graficos de Dispersión para los Residuos

-
Imagen
     Los gráficos de dispersión para los residuos son una herramienta útil para verificar los supuestos del modelo lineal simple y evaluar si los errores tienen alguna estructura sistemática. Estos gráficos muestran la relación entre los residuos y los valores ajustados del modelo.      Para hacer un gráfico de dispersión para los residuos, se grafican los residuos (eje y) versus los valores ajustados del modelo (eje x). Si el modelo es adecuado y se cumplen los supuestos, los residuos deberían distribuirse aleatoriamente alrededor de cero y no debería haber ninguna relación clara entre los residuos y los valores ajustados. Ejemplos:
Leer más

Diagrama de Dispersión

-
Imagen
     Un diagrama de dispersión es una herramienta gráfica que se utiliza para analizar la relación entre dos variables. En este tipo de diagrama, los valores de una variable se representan en el eje horizontal (eje x) y los valores de la otra variable se representan en el eje vertical (eje y).      Cada punto en el diagrama de dispersión representa una observación de las dos variables. Si los puntos están agrupados cerca de una línea recta, esto sugiere que hay una relación lineal entre las dos variables. Por otro lado, si los puntos están dispersos y no parecen seguir una línea recta, esto sugiere que no hay una relación lineal clara entre las dos variables.      El diagrama de dispersión es una herramienta muy útil para analizar la relación entre dos variables, especialmente cuando se utiliza en conjunto con otras técnicas estadísticas como el coeficiente de correlación y la regresión lineal.
Leer más